La conoscenza della matematica e la capacità di interpretare correttamente i risultati, sono dei requisiti fondamentali nella comunicazione del rischio.
Iniziamo col risolvere un veloce calcolo aritmetico, da fare a mente:
Quanto fa mille più quaranta?
Adesso aggiungete ancora mille,
e ancora trenta,
più venti,
più altri mille,
e, infine, aggiungete ancora dieci.
La maggioranza delle persone risponde 4.000, mentre la risposta corretta è 3.100.
Molti di noi possono individuare una faccia ben precisa in una folla più velocemente di quanto non sappiano rispondere a 7×8. La verità è che la maggior parte delle persone fa fatica a fare velocemente calcoli numerici.
Se diamo abbastanza numeri alle persone molte di loro avranno emozioni negative, emozioni che spesso interferiscono con la loro abilità di prendere buone decisioni.
Tali problemi matematici sono rilevanti perché, per alcune decisioni mediche molto importanti, la giusta scelta dipende dall’afferrare alcune nozioni matematiche di base nel modo corretto e forse, in nessun altro ambito medico, ci sono tanti numeri – discussione più esplicita di probabilità numeriche e sopravvivenza a cinque anni – dell’ambito dei tumori.
Lo psicologo tedesco Gerd Gigerenzer è direttore emerito del Center for Adaptive Behavior and Cognition (ABC) presso il Max Planck Institute for Human Development e direttore dell’Harding Center for Risk Literacy, entrambi a Berlino, in Germania. Gigerenzer, in un suo famoso articolo intitolato Aiutare medici e pazienti a capire le statistiche sulla salute (2007), sostiene che la comunicazione del rischio è un problema centrale per medici, pazienti, dirigenti, giornalisti e che vi sia una diffusa incapacità a comprendere il significato di informazioni numeriche.
ANALFABETISMO STATISTICO: RISCHIO RELATIVO E RISCHIO ASSOLUTO
 L’analfabetismo statistico collettivo è la diffusa inabilità di capire il significato di informazioni numeriche ed è comune a pazienti, giornalisti, medici, politici ,ecc… ed è dovuto (in parte) a formati di presentazione delle informazioni non trasparenti (intenzionalmente o meno). Può anche avere serie conseguenze per la salute.
L’analfabetismo statistico collettivo è la diffusa inabilità di capire il significato di informazioni numeriche ed è comune a pazienti, giornalisti, medici, politici ,ecc… ed è dovuto (in parte) a formati di presentazione delle informazioni non trasparenti (intenzionalmente o meno). Può anche avere serie conseguenze per la salute.
Alcune soluzioni che sono state proposte in questo senso sono le seguenti:
- Insegnare il pensiero statistico con esempi che si possano applicare a facilmente a problemi reali (non a lanci di monete e dadi).
- Promuovere l’uso di formati trasparenti di presentazione delle informazioni (per esempio, alcuni produttori di snack riferscono il dato delle calorie calcolandole su 30 grammi, ma poi il sacchetto è da 40 grammi).
- Insegnare a riconoscere (e diffidare di) formati non trasparenti e a tradurli in formati trasparenti.
Note sulla lettura dell’articolo di Gigerenzer:
- Il termine “framing” in questo contesto ha un’accezione molto più generale rispetto al termine usato in altri ambiti in riferimento all’effetto framing (che si riferisce invece al presentare informazioni in due modi contrapposti e complementari). Nell’articolo di Gigerenzer viene usato il sostantivo e il verbo (“to frame”) che letteralmente può essere tradotto come il modo di strutturare/formulare/esprimere le informazioni.
- Nell’articolo viene usata la notazione inglese dei numeri, che si differenzia da quella italiana usando punti e virgole all’opposto e in alcuni casi questo può creare confusione (es. 10,000).
Vediamo ora alcuni esempi di analfabetismo statistico.
RISCHIO RELATIVO CONTRO RISCHIO ASSOLUTO
Ann Furedi, ex amministratore delegato del British Pregnancy Advisory Service, il più grande fornitore indipendente di aborti del Regno Unito pubblica nel 1999 l’articolo Conseguenze sociali. Le implicazioni per la salute pubblica della “paura delle pillole” del 1995.
L’articolo dice quanto segue:
L’avvertimento emesso dal Comitato britannico per i medicinali di sicurezza nell’ottobre 1995, seguito dalla lettera “Caro dottore” del 18 ottobre 1995, diceva che le pillole contraccettive orali contenenti gestodene o desogestrel erano associate a un rischio maggiore di tromboembolismo venoso hanno avuto un impatto negativo sulla salute pubblica. Un numero significativo di donne ha cambiato marca o ha cessato del tutto la contraccezione dopo l’annuncio. I dati nazionali suggeriscono una forte associazione tra la paura della pillola e un aumento sostanziale del numero di gravidanze indesiderate, particolarmente significativo tra le donne più giovani, con l’uso della contraccezione orale che è sceso dal 40 al 27% tra le minori di 16 anni tra il 1995-1996 e il 1996-1997. Il costo risultante dell’aumento delle nascite e degli aborti per il Servizio sanitario nazionale è stato stimato in circa 21 milioni di sterline per l’assistenza alla maternità e da 46 milioni di sterline per l’aborto. Il livello di rischio dovrebbe, in futuro, essere valutato più attentamente e i consigli presentati con maggiore attenzione nell’interesse della salute pubblica.
L’annuncio di emergenza è stato dato dai media alla popolazione e sono state spedite 190.000 lettere a medici di base, farmacisti e direttori sanitari scrivendo che “L’uso della pillola anticoncezionale di terza generazione aumenta il rischio tromboembolico del 100%”.
Le conseguenze sono state ovvie:
 Stress, paura, preoccupazione, interruzione dell’assunzione della pillola;
Stress, paura, preoccupazione, interruzione dell’assunzione della pillola;- Aumento stimato di 13.000 aborti e altrettante gravidanze indesiderate (di cui 800 in ragazzine di 16 anni);
- Aumentato del rischio tromboembolico maggiore di quello della pillola (per aborti e gravidanze stesse);
- Costi sanitari;
- Perdita di “fiducia” nella pillola.
Gli studi originali su cui si basava la notizia avevano confrontato un gruppo di donne che prendeva la pillola di 2a generazione con un gruppo di donne che prendeva quella di 3a e i risultati erano stati i seguenti:
- Con pillola anticoncezionale di 2a generazione, numero di trombosi: 1
- Con pillola anticoncezionale di 3a generazione, numero di trombosi: 2
Effettivamente il numero di casi di trombosi era raddoppiato, in quanto il rischio relativo da 1 passa a 2, corrispondendo quindi ad un aumento relativo del 100% …ma 1 e 2 sono numeri piccoli e c’è da capire anche su quanta popolazione.
Il dato reale è il seguente:
| Pillola di 2a generazione | Pillola di 3a generazione | Rischio relativo | |
| Numero trombosi | 1 | 2 | da 1 a 2 raddoppia |
| Campione totale | 7.000 | 7.000 | |
| Rischio assoluto (0-1) | 1/7.000 = 0,014% | 2/7.000 = 0,028% | Il dato raddoppia sempre, ma la differenza è molto piccola |
Pertanto, se le autorità e i media avessero comunicato il rischio assoluto (e non il rischio relativo) avrebbero probabilmente evitato il panico scatenato dalla notizia e tutte le successive conseguenze.
Le cause del problema sono state:
- Analfabetismo statistico → Le persone faticano a distinguere tra rischio relativo e assoluto.
- Formato non trasparente → I media spesso usano il rischio relativo (numero più grande di quello assoluto, quindi più sensazionale).
Le possiibli soluzioni al problema sono:
- Alfabetizzazione statistica minima → Insegnare concetti di base di alfabetizzazione statistica alla popolazione, inclusa la differenza tra rischio relativo e rischio assoluto.
- Usare formati trasparenti → Uso del rischio assoluto (invece che relativo) da parte di autorità, media, ecc.
Il rischio relativo è sempre un esempio di formato non trasparente: è ingannevole perché considera solo il numero di eventi che si verificano (il numeratore) ma non considera per niente il numero totale degli eventi (il denominatore), che sono invece considerati nel rischio assoluto.
Due eventi con rischio assoluto molto diverso possono portare alla stessa differenza in termini di rischio relativo, per esempio da 1/1.000 a 2/1.000 il rischio relativo raddoppia (aumento del 100%), ma anche da 300/1.000 a 600/1.000 il rischio relativo raddoppia, mentre se consideriamo il rischio assuluto, nel primo caso si passa da 0,1% a 0,2% e nel secondo caso si passa dal 30% al 60%.
È quindi fondamentale saper sempre riconoscere il rischio relativo da quello assoluto:
- Il rischio relativo può essere espresso in aumento o diminuzione percentuale (es. aumento del 100% del rischio tromboembolico) o in termini comparativi verbali (es. il rischio raddoppia, si dimezza, ecc.), si riferisce sempre a due probabilità e ne esprime il rapporto.
- Il rischio assoluto invece si riferisce alla probabilità di singoli eventi, senza metterli in relazione tra loro e può essere espresso in percentuale (es. il rischio tromboembolico passa dallo 0,1% allo 0,2%) o in frequenza (es. si è passati da 1 caso su 1.000 a 2 casi su 1.000).
Un altro esempio di analfabetismo statistico è il seguente.
FALSI POSITIVI E FALSI NEGATIVI
 Molte donne partecipano a programmi di screening per il tumore al seno. Nel caso in cui la mammografia risulti positiva, significa che hanno un tumore al seno? C’è certamente un margine di errore nell’esame, ma quanto è grande? Quanto è probabile che ci sia veramente un tumore? E se lo si chiede al ginecologo, cosa risponde?
Molte donne partecipano a programmi di screening per il tumore al seno. Nel caso in cui la mammografia risulti positiva, significa che hanno un tumore al seno? C’è certamente un margine di errore nell’esame, ma quanto è grande? Quanto è probabile che ci sia veramente un tumore? E se lo si chiede al ginecologo, cosa risponde?
(Nota: lo stesso discorso vale per qualsiasi test diagnostico, come ad esempio il test dell’HIV. Un risultato positivo significa avere l’HIV? Un test FOBT positivo significa avere un tumore al colon-retto?)
Le informazioni necessarie a rispondere alla domanda “Se il test è positivo, significa che ho la malattia?” sono 3:
- la probabilità di avere la malattia (prevalence), cioè quante persone hanno la malattia nella popolazione di riferimento;
- la sensibilità del test (sensitivity), cioè la probabilità che una persona con la malattia risulti positiva al test;
- il tasso di falsi positivi (false-positive-rate), cioè la probabilità che una persona sana risulti comunque positiva;
oppure la specificità del test (specificity), che non è altro che il complemento del tasso di falsi positivi, cioè la probabilità che una persona sana risulti negativa.
A 160 ginecologi sono stati forniti i seguenti dati:
- Probabilità di avere la malattia: 1%
- Sensibilità del test: 90%
- Tasso di falsi positivi: 9%
È poi stata posta loro la seguente questione: “Una donna con risultato positivo chiede se è sicuro che abbia la malattia e, se no, quali siano le probabilità” e quindi sono state fornite 4 possibili suluzioni:
- la probabilità che abbia la malattia è circa dell’81%; (81%)
- su 10 donne con risultato positivo, 9 hanno la malattia; (90%)
- su 10 donne con risultato positivo, 1 ha la malattia; (10%)
- la probabilità che abbia la malattia è circa dell’1%. (1%)
Se ha un risultato positivo, qual è la probabilità che abbia la malattia?
I 160 ginecologi ha risposto come segue (preoccupante l’alta variabilità nelle risposte…):
- 13%
- 47%
- 21%
- 19%
La maggioranza ha risposto 90%, che corrispondente alla sensibilità del test (tra le persone ammalate, quelle che risultano positive), la risposta corretta però è 10% (risposta c). Perché la risposta giusta non è 90%? Perché la risposta giusta è 10%? E perché è così difficile da calcolare?
Vediamo innanzitutto perché è così difficile rispondere correttamente:
Perché la risposta giusta non è 1%? L’1% è la probabilità di malattia nella popolazione, quindi è una probabilità che è indipendente dal test. Chiunque potrebbe essere quella persona su 100 e si fa il test proprio per sapere se si è malati e se questa persona ha un test positivo. Non è più quindi una persona presa a caso sulle 100 e la probabilità che sia malata è più alta del 1%.
Perché la risposta giusta non è 90%? Perché 90% è la probabilità che una persona con la malattia abbia un risultato positivo al test (sensibilità del test), ma sappiamo che il test può sbagliare e c’è una probabilità del 9% che anche chi è sano risulti positivo (tasso di falsi positivi). Bisognerebbe chiedersi come sia possibile sapere se il risultato positivo è parte del 90% dei (veri) positivi di chi è malato o se è parte del 9% dei positivi (falsi) di chi è sano.
Perché la risposta giusta non è 81%? Questa risposta tiene conto dei falsi positivi (90 – 9 = 81), ma non tiene conto della prevalenza della malattia nella popolazione.
Per rispondere correttamente al quesito vanno combinate tutte e tre le informazioni usando il Teorema di Bayes.
La probabilità di avere la malattia “condizionata” al fatto che il test è risultato positivo si indica come:
p ( malato | positivo)
È anche chiamata valore positivo predittivo (positive predictive value).
IL TEOREMA DI BAYES
Thomas Bayes (1702-1961), matematico e ministro presbiteriano britannico, propose la seguente formula per trovare il corretto valore predittivo:
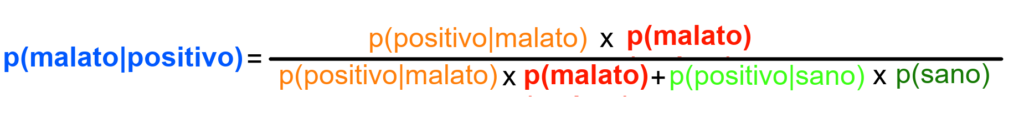
Dove il dato che vogliamo conoscere è p(malato|positivo) = probabilità che la persona sia ammalata sapendo che il test ha avuto un esito positivo.
I dati che invece conosciamo sono:
p(malato) = probabilità che qualsiasi persona sia malata (1%)
p(positivo|malato) = probabilità che il test sia positivo se una persona è ammalata (90%) – sensibilità
p(positivo|sano) = probabilità che il test sia positivo se una persona è sana (9%) falso positivo
p(sano) = probabilità che qualsiasi persona sia sana (%)
Sostituiamo ora con le probabilità numeriche, traduciamo le percentuali in probabilità (range 0-1):
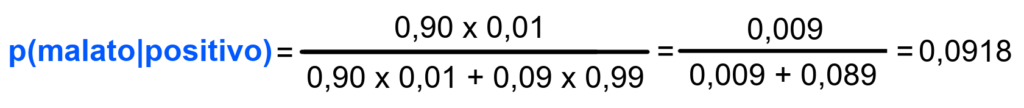
Quindi la risposta corretta era effettivamente ≈ 10%.
La maggior parte delle malattie per le quali si fa un test diagnostico non sono molto frequenti e nell’esempio della mammografia, la malattia aveva una probabilità dell’1%. La probabilità che l’esito positivo indicasse un tumore al seno (con test con sensibilità del 90% e specificità del 91%) era circa del 10%, ciò significa che su 1.000 donne, 98 risultano positive, 9 sono effettivamente malate, le altre 89 vengono allarmate ma sono sane (falsi positivi).
Chiunque partecipi ad uno screening deve essere informato del fatto che la maggior parte dei risultati positivi sono falsi allarmi.
“Ci troviamo di fronte ad un problema etico su larga scala per il quale esiste già una soluzione efficiente che i comitati etici, concentrando la loro attenzione sulle cellule staminali, sull’aborto e su altre questioni che invitano a dibattiti infiniti, non hanno ancora notato” (Gigerenzer et al., 2007).
CAPIRE MEGLIO LA PROBABILITÀ CONDIZIONATA
Ritornando al discorso dell’analfabetismo statistico, si capisce che la probabilità condizionata è ancora più difficile da calcolare di altre statistiche, molto poco intuitiva, e anche gli esperti, a tal proposito, sono in difficoltà.
Per capire meglio la formula del Teorema di Bayes e capire come applicarla senza bisogno di averla a disposizione, dobbiamo capire meglio la probabilità condizionata. A parte la complessità della formula, il concetto è semplice: i risultati positivi possono essere veri positivi (malati con risultato positivo) o falsi positivi (sani con risultato positivo).
La formula non fa altro che calcolare:
- al numeratore i veri positivi (cioè quanti dei malati sono positivi)
- al denominatore tutti i risultati positivi (veri + falsi, cioè quanti dei sani sono comunque positivi)
Un altro modo per rappresentare lo stesso problema è con un grafico ad albero, come il seguente e seguendo gli stessi passaggi:

- Probabilità malattia → malati e sani
- Sensibilità applicata a malati → veri positivi e falsi negativi
- Specificità applicata a sani → falsi positivi e veri negativi
- Ora abbiamo tutti i dati e possiamo sapere quanti dei positivi sono veri
Seguendo l’ordine dei dati:
- Il 90% (positivo) di 1% (cancro al seno) = 0,9%
- Il 10% (negativo) di 1% (cancro al seno) = 0,1%
- Il 9% (positivo) di 99% (no cancro al seno) = 8,9%
- Il 91% (negativo) di 99% (no cancro al seno) = 90.1%
0.9% / (0,9% + 8.9%) = 0,0918 → 9,18%
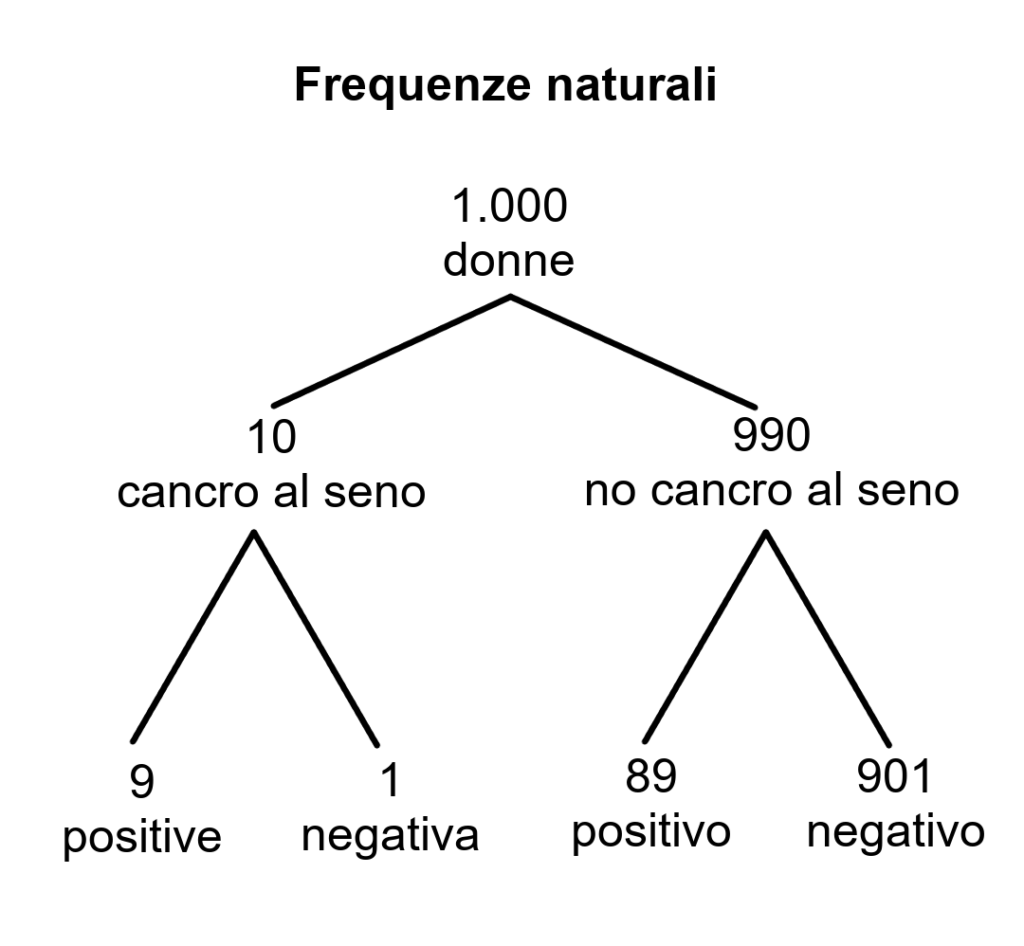 Secondo Gigerenzer le percentuali sono un formato non trasparente e rendono difficile il problema, mentre se invece si usassero le frequenze naturali (formato trasparente), il problema sarebbe ancora di più facile soluzione.
Secondo Gigerenzer le percentuali sono un formato non trasparente e rendono difficile il problema, mentre se invece si usassero le frequenze naturali (formato trasparente), il problema sarebbe ancora di più facile soluzione.
Questo metodo semplifica il calcolo perché si ha a che fare con numeri di persone (frequenze naturali) e non probabilità, anche se bisogna comunque “tradurre” le probabilità in frequenze naturali.
Su 1000 donne, 98 risultano positive, 9 sono effettivamente malate, le altre 89 vengono allarmate ma sono sane (falsi positivi).
9 / (9 + 89) = 0,0918 → 9,18%
L’ILLUSIONE DI CERTEZZA
I pazienti devono essere informati del fatto che anche i migliori test non sono perfetti e che ogni risultato di un test deve essere interpretato. Alcuni test sono più “pericolosi” di altri e hanno bisogno di essere trattati con particolare cura (come il test dell’HIV).
Vediamo un caso:
 A 22 donatori di sangue americani della Florida è stato notificato che erano risultati positivi al test ELISA (uno dei test per l’HIV).
A 22 donatori di sangue americani della Florida è stato notificato che erano risultati positivi al test ELISA (uno dei test per l’HIV).
In seguito a tale notifica, sette di loro si sono suicidati.
Un documento medico riguardo a questo caso ha poi calcolato che anche se i risultati di entrambi i test per l’AIDS (cioè il test ELISA e il Western blot) sono positivi, le probabilità di essere infettati veramente per le persone a basso rischio (come i donatori di sangue) sono comunque solo del 50%. (Stine, 1999, p. 367).
In realtà il test ha bassissimi margini di errore, infatti ha un’altissima sensibilità alla malattia (≈ 99.9%) e anche un’altissima specificità (≈ 99.9% a seconda dei criteri), ma un enorme peso ce l’ha la probabilità della malattia nella popolazione di riferimento. Nelle persone a basso rischio infatti (come i donatori di sangue eterosessuali) la probabilità della malattia è molto bassa, nell’ordine di 1 persona ogni 10.000.
Dato che la probabilità della malattia nella popolazione è estremamente bassa (1 su 10,000 cioè 0,01%), il valore positivo predittivo, cioè la probabilità che un esito positivo al test indichi effettivamente la malattia è il 50%.
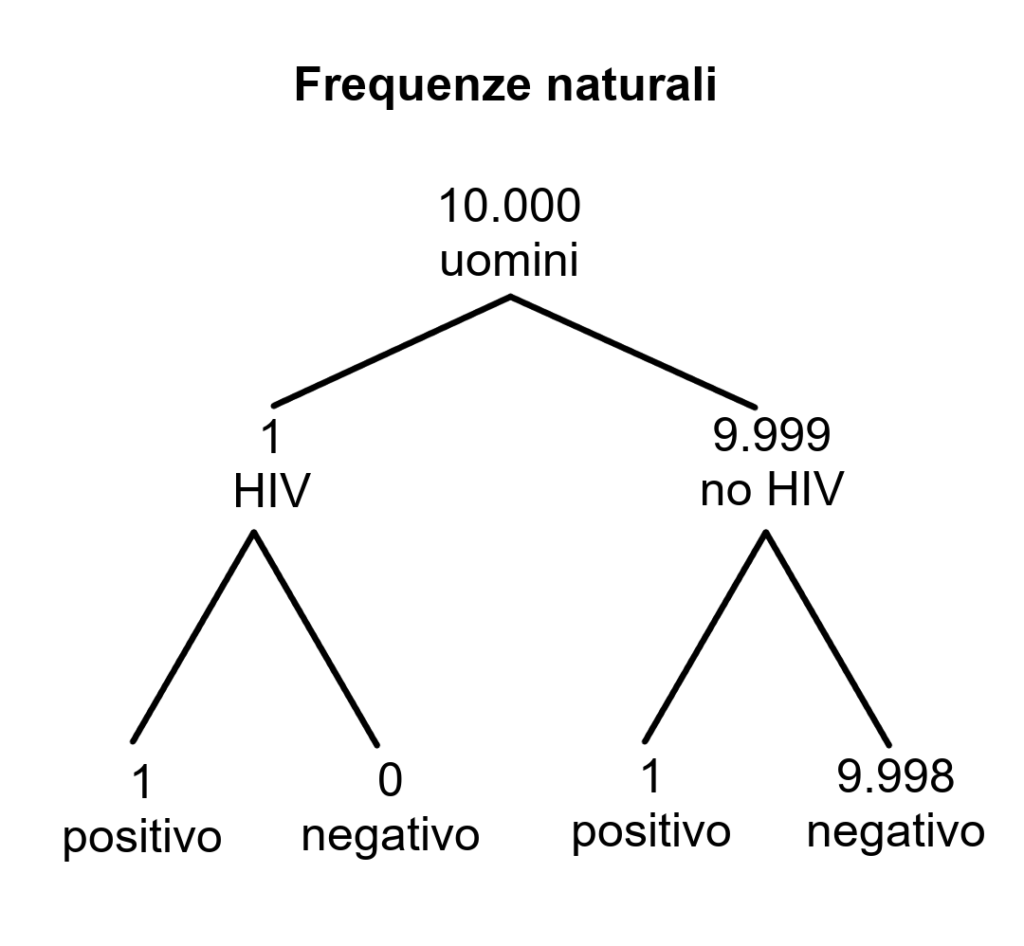 Se descriviamo questo risultato in termini di frequenze naturali, diventa molto più chiaro:
Se descriviamo questo risultato in termini di frequenze naturali, diventa molto più chiaro:
Su 10,000 persone, 1 è infetta ed è estremamente probabile che risulti positiva al test, ma anche 1 persona delle 9,999 che non hanno la malattia risulterà positiva. Quindi il valore positivo predittivo è del 50% (1 su 2).
Ovviamente i counselor che si occupano di AIDS dovrebbero informare adeguatamente chiunque faccia il test. Ma lo fanno? Fingendosi un paziente, una persona ha consultato 20 centri pubblici di consulenza per l’HIV in Germania. Ha sempre detto chiaramente di non essere a rischio e a tutti i couselor ha chiesto: “C’è la possibilità che io abbia un risultato positivo anche se non ho il virus? Se sì, quanto spesso succede?”. Dei 20 counselor consultati, 13 danno un’illusione di certezza (“Certamente no”, “Impossibile”, “Il test è assolutamente certo”), 3 all’inizio danno una certezza ma poi lasciano spazio a un minimo dubbio (Definitivamente no…. è estremamente raro”, “Assolutamente no… ha una specificità del 99,9%”), altri 3 dicono subito che possono esserci dei falsi positivi, ma citano statistiche solo sulla specificità, non sul valore predittivo positivo (“La specificicità è oltre il 99%”), 1 ha semplicemente risposto “Fidati”.
Si è creduto che le impronte digitali fossero a” prova d’errore” fino al 1998 quando l’FBI spedì a diversi uffici giudiziari due impronte scoperte su una macchina rubata perché le confrontassero con quelle della persona sospettata per il furto. Su 35 laboratori 8 non riuscirono a trovare una corrispondenza per la prima impronta, 6 non la trovarono per la seconda. Il sistema è quindi tutt’altro che infallibile: uno studio del 2011 ha riscontrato una percentuale di falsi positivi pari allo 0,1%. (impronte che risultano coincidere anche se in realtà non sono uguali). Potrebbe sembrare una percentuale risibile, ma non lo è.
Nessun test fornisce esiti assolutamente certi.Oltre alle caratteristiche del test conta molto la probabilità della malattia nella popolazione di riferimento, che spesso è bassa. È fondamentale capire che i test di screening possono produrre due errori: falsi positivi e falsi negativi. La difficoltà del calcolare le probabilità condizionate sono comprensibili (anche se dagli esperti ci si aspetterebbe che siano in grado di calcolare tali statistiche). Serve educazione al riconoscimento delle probabilità condizionate e alla traduzione in formati più trasparenti.
MORTALITÀ CONTRO SOPRAVVIVENZA
 Durante la campagna per le primarie del 2007, l’ex sindaco di New York, Rudy Giuliani, disse: ‘‘Cinque-sei anni fa ho avuto il cancro alla prostata. Quante erano le mie probabilità di sopravvivere (per fortuna sono guarito) qui, negli States? Erano dell’ 82%. E se fossi vissuto nel Regno Unito? Sarebbero state solo del 44%”.
Durante la campagna per le primarie del 2007, l’ex sindaco di New York, Rudy Giuliani, disse: ‘‘Cinque-sei anni fa ho avuto il cancro alla prostata. Quante erano le mie probabilità di sopravvivere (per fortuna sono guarito) qui, negli States? Erano dell’ 82%. E se fossi vissuto nel Regno Unito? Sarebbero state solo del 44%”.
Per Giuliani queste statistiche significavano che era fortunato a vivere a New York e non a York, dato che le probabilità di sopravvivere al cancro sembravano il doppio.
I dati a cui si riferiva Giuliani (relativi al 2000) erano:
- Nel Regno Unito, a 44.000 uomini su 100.000 era stato diagnosticato un tumore alla prostata. La sopravvivenza a 5 anni era del 44%.
- In America, l’ 82% degli americani che avevano avuto la stessa diagnosi erano ancora vivi dopo 5 anni.
La differenza sta nel modo in cui viene eseguita la diagnosi: in Inghilterra la diagnosi è basata principalmente sui sintomi, mentre in America è basata principalmente sul test di screening del PSA (antigene prostata-specifico, esame del sangue).
 Come si calcola la sopravvivenza? La statistica sopravvivenza a 5 anni è la più usata quando si parla di tumore ed è data da:
Come si calcola la sopravvivenza? La statistica sopravvivenza a 5 anni è la più usata quando si parla di tumore ed è data da:
- tempo 0 → gruppo di pazienti che riceve la diagnosi
- tempo 1 → quanti pazienti sono ancora vivi 5 anni dopo?
Il problema nel comparare la sopravvivenza tra US e UK è che usano due metodi di diagnosi diversi e questo fatto influenza quando e quante persone sono diagnosticate, informazione che viene considerata nel calcolare il tasso di sopravvivenza.
Lo screening altera il tasso di sopravvivenza in due modi, influenzando:
- il momento della diagnosi iniziale (il quando)
- la natura della diagnosi (il quanto)
Consideriamo lo stesso gruppo di pazienti che muoiono a 70 anni:
- con diagnosi basata sui sintomi (come in UK), la malattia è trovata tardi, es. a 67 anni. La sopravvivenza a 5 anni è di 0%;
- con diagnosi basata su screening (come in US) è prima, poniamo a 60 anni. La sopravvivenza a 5 anni è del 100%.
Sembra che lo screening aumenti la sopravvivenza, MA tutti muoiono alla stessa età (lead-time bias).
Nel gruppo dei “malati di cancro” sono inclusi anche i pazienti con tumori non mortali e non progressivi, che non causerebbero mai sintomi. Rispetto alla diagnosi basata su sintomi, con lo screening sono diagnosticate anche molte altre persone con tumori non progressivi. Siccome tutti sopravvivono, vanno a “gonfiare” il numero dei sopravvissuti (overdiagnosis bias).
Per confrontare il successo contro il cancro in due paesi che usano diversi sistemi diagnostici è necessario usare una statistica che si riferisce alla mortalità.
 tempo 0 → tutte le persone che potrebbero avere la malattia (in questo caso uomini – la diagnosi non è nota)
tempo 0 → tutte le persone che potrebbero avere la malattia (in questo caso uomini – la diagnosi non è nota)- tempo 1 → quante persone sono morte di cancro un anno dopo
Infatti, se guardiamo ai dati dei due paesi il tasso di sopravvivenza è effettivamente diverso mentre il tasso di mortalità resta sostanzialmente uguale:
| Diagnosi basata sui sintomi (UK) | Diagnosi basata sullo screening (US) | |
| Numero vivi a 5 anni | 440 | 2.440 |
| Numero diagnosi | 1.000 | 3.000 |
| Sopravvivenza (a 5 anni) | 44% | 81% |
| Numero morti (a 1 anno) | 27 | 26 |
| Numero totale popolazione | 100.000 | 100.000 |
| Mortalità (a 1 anno) | 27/100.000 = 0,027% | 27/100.000 = 0,026% |
Così come il rischio relativo mostra solo un pezzo della storia (ignorando il numero totale di eventi), anche il tasso di sopravvivenza mostra solo un pezzo della storia, focalizzandosi sulle persone con diagnosi. Con metodi di diagnosi diversi il tasso di sopravvivenza non è comparabile, il tasso di mortalità lo è perché considera il numero di morti nella popolazione, che non è influenzato dal metodo di diagnosi.
Le cause del problema restamo sempre l’analfabetismo statistico e il formato non trasparente (forse intenzionale).
CONCLUSIONI
Abbiamo visto tre esempi concreti di analfabetismo statistico:
- pillola anticoncezionale → rischio relativo contro rischio assoluto
- mammografia di screening → falsi positivi e falsi negativi
- cancro della prostata → mortalità contro sopravvivenza
Questi esempi illustrano come l’analfabetismo statistico sia diffuso (pazienti, medici, politici, giornalisti), come possa avere conseguenze gravi (es., aborti, stress, voto) e come sia spesso basato su informazioni non trasparenti.
“Inquadrare le informazione in un modo che sia più facilmente compreso dalla mente umana è un primo passo verso l’educare medici e pazienti all’alfabetizzazione al rischio.” (Gerd Gigerenzer)
FONTI:
- Furedi A. Social consequences. The public health implications of the 1995 ‘pill scare’. Human Reproduction Update, Volume 5, Issue 6, November 1999, Pages 621–626, https://doi.org/10.1093/humupd/5.6.6
- Gigerenzer G., Gaissmaier W., Kurz, Milcke E., Scwartz L.M., Woloshin S. (2007). Helping Doctors and Patients Make Sense of Health
Statistics. Psychological Science in the Public Interest, 8 (2), 53896. - Gigerenzer, G. (2007). Gut feelings: The intelligence of the unconscious. New York: Viking.
- Gigerenzer, G., Hoffrage, U., & Ebert, A. (1998). AIDS counselling for low-risk clients. AIDS Care, 10, 197–211.
- Lotto L. A.A. (2021-22). Articolo Gigerenzer et al. (2007) – Lezioni di Comunicazione del rischio e processi decisionali – Dipartimento di Psicologia dello Sviluppo e della Socializzazione dell’Università di Padova.
- Stine, G.J. (1999). AIDS update 1999: An annual overview of acquired immune deficiency syndrome.Upper Saddle River, NJ: Prentice-Hall.